STATISTICS (LECTURE 8)

Good morning Boys...............

Today's learning outcome :

The two methods of Ogives are

• Less than Ogive
• Greater than or more than Ogive

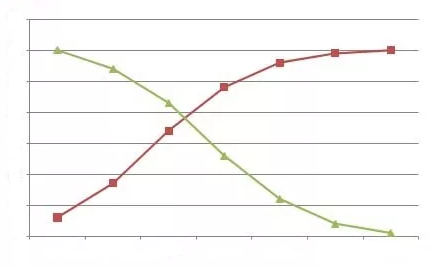
The graph given above represents less than and the greater than Ogive curve. The rising curve (Brown Curve) represents the less than Ogive, and the falling curve (Green Curve) represents the greater than Ogive.

Less than Ogive

The frequencies of all preceding classes are added to the frequency of a class. This series is called the less than cumulative series. It is constructed by adding the first-class frequency to the second-class frequency and then to the third class frequency and so on. The downward cumulation results in the less than cumulative series.

Greater than or More than Ogive

The frequencies of the succeeding classes are added to the frequency of a class. This series is called the more than or greater than cumulative series. It is constructed by subtracting the first class second class frequency from the total, third class frequency from that and so on. The upward cumulation result is greater than or more than the cumulative series.

Ogive Chart

An Ogive Chart is a curve of the cumulative frequency distribution or cumulative relative frequency distribution. For drawing such a curve, the frequencies must be expressed as a percentage of the total frequency. Then, such percentages are cumulated and plotted as in the case of an Ogive. Here, the steps for constructing the less than and greater than Ogive are given.

How to Draw Less Than Ogive Curve?

• Draw and mark the horizontal and vertical axes.
• Take the cumulative frequencies along the y-axis (vertical axis) and the upper-class limits on the x-axis (horizontal axis).
• Against each upper-class limit, plot the cumulative frequencies.
• Connect the points with a continuous curve.

How to Draw Greater than or More than Ogive Curve?

• Draw and mark the horizontal and vertical axes.
• Take the cumulative frequencies along the y-axis (vertical axis) and the lower-class limits on the x-axis (horizontal axis).
• Against each lower-class limit, plot the cumulative frequencies
• Connect the points with a continuous curve.

Uses of Ogive Curve

Ogive Graph or the cumulative frequency graphs are used to find the median of the given set of data. If both the less than and the greater than cumulative frequency curve is drawn on the same graph, we can easily find the median value. The point in which both the curve intersects, corresponding to the x-axis gives the median value.  Apart from finding the medians, Ogives are used in computing the percentiles of the data set values.

we will do more than type OGIVE.

For this we need to calculate more than cf

Click on the Link to know about it

Look at example☟

In the given frequency table , we will find more than cf

We will use lower limits of the class intervals where as we used upper limits in less than ogive

1.  start from the bottom most frequency , last cf and frequency will be same.

2. As we move up, we will keep adding frequencies  

cf₁ =8 

cf₂ =8 +7

cf₃ = 8+7 +9

.

.

.

last cf = total of all frequencies=53

And we will get ☟ (Complete the table)

Marks obtained	Number of students (Cumulative frequency
More than or equal to 0	53
More than or equal to 10
More than or equal to 20
More than or equal to 30
More than or equal to 40
More than or equal to 50
More than or equal to 60
More than or equal to 70
More than or equal to 80
More than or equal to 90	8

Why did we write in the ↑ table " More than equal to" when we used " less than" in the first type of ogive ?

Next step is to draw more than ogive

Click on the link to view it.

Note down Q3 of EX 14.4

3. The following tables gives production yield per hectare of wheat of 100 farms of a village.

Production Yield	50-55	55-60	60-65	65-70	70-75	75-80
Number of farms	2	8	12	24	38	16

Change the distribution to a more than type distribution and draw its ogive.

Solution:

✬✬  In case data is not continuous, then convert it to the required form.

 Converting the given distribution to a more than type distribution, we get

Production Yield (kg/ha)	Number of farms(cf)
More than or equal to 50	100
More than or equal to 55	98
More than or equal to 60	90
More than or equal to 65	78
More than or equal to 70	54
More than or equal to 75	16

From the table obtained draw the ogive by plotting the corresponding points where the lower limits  in x-axis and the frequencies obtained in the y-axis are (50, 100), (55, 98), (60, 90), (65, 78), (70, 54) and (75, 16) on this graph paper. The graph obtained is known as more than type ogive curve.

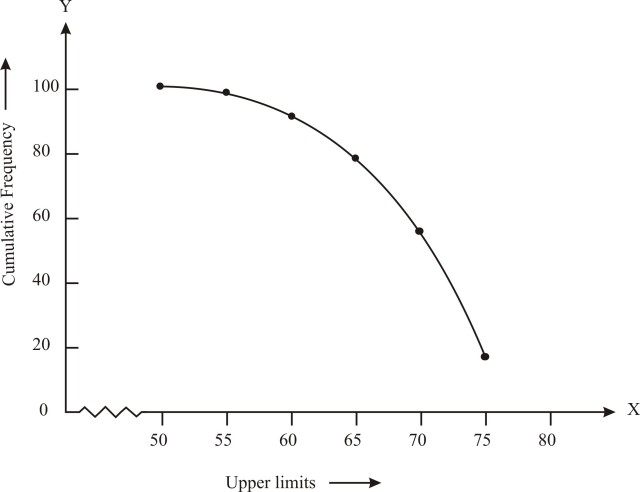
How to find median from more than ogive( It is similar to what we did  in less than ogive)
Look at the more than ogive☟

1. Find N/2 = 200/2= 100 
 2. Now, draw a perpendicular from  the division 100(along y axis) to  cut the Ogive curve at point A.

3. From point A where the Ogive curve is cut, draw a perpendicular on the x-axis. The point at which it touches the x-axis will be the median value of the series as shown in the graph.

(Is it not similar ?? )

How to find Median using both types of ogive on the same axis

In this case,we will draw a perpendicular from the point of inetrsection A (of the two ogives).
The point at which the perpendicular cuts the Xaxis is the MEDIAN

Question  for CW

 Q1The annual rainfall record of a city for 66 days if given in the following table:

Rainfall (in cm):	0-10	10-20	20-30	30-40	40-50	50-60
Number of days:	22	10	8	15	5	6

Calculate the median rainfall using ogives of more than type and less than type.

✴✴ Yesterday , you had drawn less than ogive for the same question(as HW)

Now, you can continue from there.

Question for HW

Question 1

Draw more than type of ogive and then  calculate median .

Question 2The annual profits earned by 30 shops of a shopping complex in a locality give rise to the following distribution 

Draw both ogives for the data above. Hence obtain the median profit.

Today's class ends here!!

There will be a test from statistics on Monday!!