STATISTICS (LECTURE 7)

LESSON  STATISTICS

Dear Students,

Good Morning !!

Yesterday we covered the following learning outcomes:

1 . Recall ,measures  of central tendency.

2 .calculating Mean, Median and Mode.

Let us go through the guidelines for the  blog once again:

•              The text in Red, is to be written in your register

•              The text in blue is to be viewed by clicking on it

•              The text in green is to be practised for home work

General Instructions

•               take your SET-A Mathematics Register

.               Please write the learning outcomes as mentioned below:

                I will be able to  :

•                   draw a less  than type  ogive and find its median

•                draw a  more than type  ogive and find its median     

Cumulative

Cumulative means "how much so far".

Think of the word "accumulate" which means to gather together.

To have cumulative totals, just add up the values as you go.

Example: Jamie has earned this much in the last 6 months:

Month	Earned
March	$120
April	$50
May	$110
June	$100
July	$50
August	$20

To work out the cumulative totals, just add up as you go.

The first line is easy, the total earned so far is the same as Jamie earned that month:

Month	Earned	Cumulative
March	$120	$120

But for April, the total earned so far is $120 + $50 = $170 :

Month	Earned	Cumulative
March	$120	$120
April	$50	$170

And for May we continue to add up: $170 + $110 = $280

Month	Earned	Cumulative
March	$120	$120
April	$50	$170
May	$110	$280

Do you see how we add the previous month's cumulative total to this month's earnings?

Here is the calculation for the rest:

• June is $280 + $100 = $380
• July is $380 + $50 = $430
• August is $430 + $20 = $450

And this is the result

Month	Earned	Cumulative
March	$120	$120
April	$50	$170
May	$110	$280
June	$100	$380
July	$50	$430
August	$20	$450

The last cumulative total should match the total of all earnings:

$450 is the last cumulative total ...

... it is also the total of all earnings:

$120+$50+$110+$100+$50+$20 = $450

So we got it right.

So that's how to do it, add up as you go down the list and you will have cumulative totals.

We could also call it a "Running Total"

so let us answer to the question given below

What is Cumulative Frequency ?

The frequency is the number of times an event occurs within a given scenario. Cumulative frequency is defined as the running total of frequencies. It is the sum of all the previous frequencies up to the current point. It is easily understandable through a Cumulative Frequency Table.

Marks	Frequency (No. of Students)	Cumulative Frequency
0 – 5	2	2
5 – 10	10	12
10 – 15	5	17
15 – 20	5	22

Cumulative Frequency Curve

Cumulative Frequency Curve

A curve that represents the cumulative frequency distribution of grouped data on a graph is called a Cumulative Frequency Curve or an Ogive. Representing cumulative frequency data on a graph is the most efficient way to understand the data and derive results.

There are two types of Cumulative Frequency Curves (or Ogives) :

• More than type Cumulative Frequency Curve
• Less than type Cumulative Frequency Curve

More Than Type Cumulative Frequency Curve

Here we use the lower limit of the classes to plot the curve.

How to plot a More than type Ogive:

1. In the graph, put the lower limit on the x-axis
2. Mark the cumulative frequency on the y-axis.
3. Plot the points (x,y) using lower limits (x) and their corresponding Cumulative frequency (y)
4. Join the points by a smooth freehand curve. It looks like an upside down S.

click the link for ogive  cumulative frequency curve or ogive

Less Than Type Cumulative Frequency Curve

Here we use the upper limit of the classes to plot the curve.

How to plot a Less than type Ogive:

1. In the graph, put the upper limit on the x-axis
2. Mark the cumulative frequency on the y-axis.
3. Plot the points (x,y) using upper limits (x) and their corresponding Cumulative frequency (y)
4. Join the points by a smooth freehand curve. It looks like an elongated S

CLICK THE LINK  TO FIND MEDIAN FROM AN OGIVE

Now quickly  answer the following questions :-

 Q1. Construction of a cumulative frequency table is useful determining the

        1.   mean

        2.   mode

        3.   median

        4.   all of the above

CLASS WORK 

Q3 .  Draw a less than type and more than type ogive for the given table and also find the median ( from the graph )  ALSO VERIFY  THE RESULT BY USING MEDIAN  FORMULA 

t 

Classes	Frequencies
0-10	12
10-20	16
20-30	17
30-40	13
40-50	11
50-60	19

EXERCISE 14.4 (HOME WORK)

1. The following distribution gives the daily income of 50 workers if a factory. Convert the distribution above to a less than type cumulative frequency distribution and draw its ogive.

Daily income in Rupees	100-120	120-140	140-160	160-180	180-200
Number of workers	12	14	8	6	10

SOLUTION 1

 Convert the given distribution table to a less than type cumulative frequency distribution, and we get

Daily income	Frequency	Cumulative Frequency
Less than 120	12	12
Less than 140	14	26
Less than 160	8	34
Less than 180	6	40
Less than 200	10	50

From the table plot the points corresponding to the ordered pairs such as (120, 12), (140, 26), (160, 34), (180, 40) and (200, 50) on graph paper and the plotted points are joined to get a smooth curve and the obtained curve is known as less than type ogive curve

2. During the medical check-up of 35 students of a class, their weights were recorded as follows:

Weight in kg	Number of students
Less than 38	0
Less than 40	3
Less than 42	5
Less than 44	9
Less than 46	14
Less than 48	28
Less than 50	32
Less than 52	35

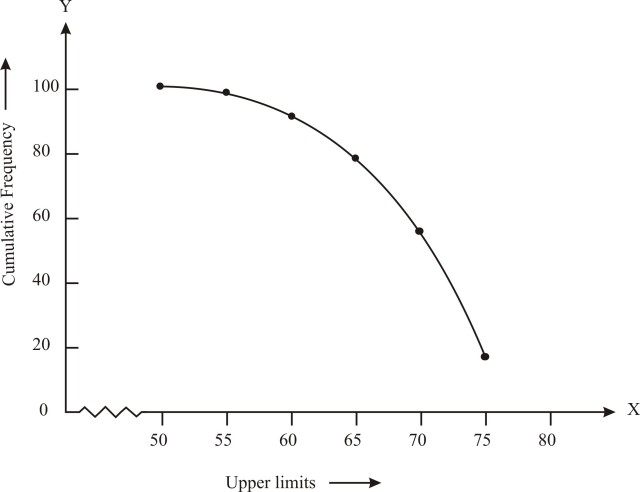
Draw a less than type ogive for the given data.

Hence obtain the median weight from the graph and verify the result by using the formula.

Solution 2: 

From the given data, to represent the table in the form of graph, choose the upper limits of the class intervals are in x-axis and frequencies on y-axis by choosing the convenient scale.

Now plot the points corresponding to the ordered pairs given by (38, 0), (40, 3), (42, 5), (44, 9),(46, 14), (48, 28), (50, 32) and (52, 35) on a graph paper an join them to get a smooth curve. The curve obtained is known as less than type ogive.

Locate the point 17.5 on the y-axis and draw a line parallel to the x-axis cutting the curve at a point. From the point, draw a perpendicular line to the x-axis.

The intersection point perpendicular to x-axis is the median of the given data.

MEDIAN = 46.5

Now, to find the MEDIAN  by making a table.

Class interval	Number of students(Frequency)	Cumulative Frequency
Less than 38	0	0
Less than 40	3-0=3	3
Less than 42	5-3=2	8
Less than 44	9-5=4	9
Less than 46	14-9=5	14
Less than 48	28-14=14	28
Less than 50	32-28=4	32
Less than 52	35-22=3	35

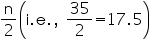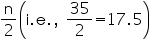Now the cumulative frequency just greater than  is 28 belonging to class interval 46 -  48

Median class = 46 - 48

Lower class limit (l) of median class = 46

Frequency (f) of median class = 14

Cumulative frequency (cf) of class preceding median class = 14

Class size (h) = 2

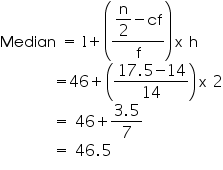
So median of this data is 46.5

Hence, value of median is verified.

3. The following tables gives production yield per hectare of wheat of 100 farms of a village.

Production Yield	50-55	55-60	60-65	65-70	70-75	75-80
Number of farms	2	8	12	24	38	16

Change the distribution to a more than type distribution and draw its ogive.

Solution:

 Converting the given distribution to a more than type distribution, we get

Production Yield (kg/ha)	Number of farms
More than or equal to 50	100
More than or equal to 55	100-2 = 98
More than or equal to 60	98-8= 90
More than or equal to 65	90-12=78
More than or equal to 70	78-24=54
More than or equal to 75	54-38 =16

From the table obtained draw the ogive by plotting the corresponding points where the upper limits in x-axis and the frequencies obtained in the y-axis are (50, 100), (55, 98), (60, 90), (65, 78), (70, 54) and (75, 16) on this graph paper. The graph obtained is known as more than type ogive curve.

AQAD

QUESTION

  The abscissa of the point of intersection of the ‘less than type’ and of the ‘more than type’ cumulative frequency curve of grouped data gives

      1.   mode

      2.   median

      3.   mean      4.   all of the above

    That's all for today  I know that this is quite a lot at once  but try to cover this in the double period. Tomorrow we will do more questions on this topic and it will become clearer.

please ask me if you have doubts in the topic.

!

   Good Morning and Thank you boys !  😊

Th