STATISTICS: MEDIAN 1(LECTURE 5)

Lesson :-STATISTICS: MEDIAN 1

Dear students


“All the statistics in the world can't measure the warmth of a smile.”
― Chris Hart


Good morning.................

In the previous classes we covered the following learning outcomes:

What is measures of central tendency?
How to calculate mode of a given data by using formula.

Let us go through the guidelines for the  blog once again:• The text in Red, is to be written in your register• The text in blue is to be viewed by clicking on it• The text in green is to be practiced for home work

1. Take your SET-A mathematics register.
2.   Our handwriting reflects a lot about us. It will be awesome if you use good presentation and cursive hand writing.
3.  Make a column on the right hand side, if you need to do any rough work.
4.   Leave two lines where you finished yesterday’s work and draw a horizontal line.

Please write the expected learning outcomes of today's class.

I will be able to 

• recall what is measure of central tendency

• median of un grouped data

• calculate the median of grouped data     

What is MEDIAN?The Median is the middle value of a distribution i.e., median of a distribution is the value of the observation which divides it into two equal parts.
In class IX you have learnt to find median of ungrouped data.

Let us do revision on ungrouped data.

How to Find the Median of Ungrouped Data

To calculate the median of a set of data, the observations are arranged in ascending or descending order and then the middle or central value of the set of observations gives us the median of data.

Based upon a number of observations, two cases can arise i.e. either the total number of observations will be odd or they would be even. Median in both the cases is determined using a different formula.

When the set of data has an odd number of observations then;

When the set of data has even number of observations then the median is;

Median = Mean of (n/2)^th and [(n/2) + 1]^th observations

Let us look into an example to understand the concept of median properly.

Example 1:Write the median of the following data3,5,2,9,7,11.soln:

let us write this data in ascending order

2,3,5,7,9,11

number of observations(n)= 6(even)

⟹ Median = (n/2)th term+ (n/2 +1)th term

                                    2

⟹(6/2)th term + (6/2 +1)th term

                      2

= 3rd term +4th term

                 2

= 5+7

     2

Therefore, Median = 6

Example 2:-Find the median of the following score obtained by a student. 37,31,42,43,46,25,39,43,42.
soln: 

Here (n) = 9(odd)

First step is the same , 

Ascending order:- 25, 31, 37, 39, 42, 42, 43, 43, 46.

Since n is odd,  Median = (n+1)/2 th term

                                         = (9+1)/2 th term

                                         = 5th term

 that is ,           Median    = 42

Now let us see how to obtain median of grouped data

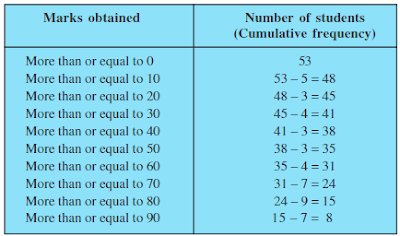
Consider a grouped frequency distribution of marks obtained ,out of 100,by 53 students in a certain examination, as follows:

How many students have scored marks less than 10? The answer is clearly 5.

How many students have scored less than 20 marks? Observe that the number of students who have  scored less than 20 include the number of students who have scored marks from 0-10 as well as the number of students  who have scored marks from 10-20. So the total number of students with marks less than 20 is 5+3=8. We say that the CUMULATIVE FREQUENCY of the class 10-20 is 8. 

Similarly, we can compute the cumulative frequencies of other classes..........

THE DISTRIBUTION GIVEN ABOVE IS called the cumulative frequency distribution of the LESS THAN TYPE.

We can similarly make the table for the number of students with scores, more than or equal to 0, more than or equal to 10, more than or equal to 20, and so on. 

The  table  above  is  called  a  cumulative  frequency  distribution  of  the  MORE THAN TYPE. Here 0, 10, 20, . . ., 90 give the lower limits of the respective class intervals. 

Now,  to  find  the  median  of  grouped  data,  we  can  make  use  of  any  of  these cumulative frequency distributions.

Now in a grouped data, we may not be able to find the middle observation by

looking at the cumulative frequencies as the middle observation will be some value in a class interval. It is, therefore, necessary to find the value inside a class that divides the whole distribution into two halves. But which class should this be? 

To find this class, we find the cumulative frequencies of all the classes and n/2. We now locate the class whose cumulative frequency is greater than (and nearest to) n/2 ⋅ This is called the MEDIAN CLASS. In the distribution above, n = 53. So, n/2 = 26.5. Now 60 – 70 is the class whose cumulative frequency 29 is greater than (and nearest to) n/2 , i.e., 26.5

Note : Do the above example in your register.

:https://www.youtube.com/watch?v=z61CKdfRdkI

click the above link to watch how to calculate the  median of grouped data.

On the basis of this video and the above example, now you are able to solve questions from exercise 14.3.
Homework for today EX 14,3 Q 1, 5. 6, and 7.


AQAD 

Q. If the mean of 4 numbers, 2,6,7 and a is 15 and also the mean of other 5 numbers, 6, 18 , 1, a, b is 50. What is the value of b?

That's all for today!!!!!!!!!!!

Good morning and thank you boys

See you after Easter holidays.......